Einer der einflussreichsten Epochen der Mathematikgeschichte ist das Zeitalter des deutschen Mathematikers Carl Friedrich Gauss. Gauss ist bekannt für seine bedeutenden Leistungen in der Arithmetik, Geometrie und astronomischen Forschung. Eines seiner wichtigsten Beiträge in der Mathematik war seine Entdeckung des sogenannten “Gauss-Verfahrens”. Im Grunde stellt dieses Verfahren eine Methode dar, mit welcher auf geometrische oder andere Weise Strukturen beschrieben und analysiert werden können. In seinem vereinfachten Modell, dem sogenannten Dreiecksformel nach Gauss, findet sich ein einfaches und zugleich mächtiges mathematisches Werkzeug, welches für eine Reihe an Anwendungsbereichen zur Problemlösung herangezogen werden kann.
Das Gauss-Verfahren
Das Gauss-Verfahren ist eine axiomatische Grundlage entwickelt, um mathematische Begriffe direkt und klar zu definieren. Zudem nutzt es neue Techniken, um komplexe Aufgaben über eine einheitliche und allgemein anerkannte mathematische Syntax zu lösen. Mit anderen Worten fördert es die konsistente Umsetzung von mathematischen Ideen in einer Weise, die sehr leicht verstanden werden kann. Für verschiedene Anwendungsbereiche wie Geometrie, algebraische Untersuchungen oder Computer-Programmierung ist es ein sehr nützliches Tool.
 Ein elegantes Beispiel ist die einfache Visualisierung namens “Basical Representation of Gauss-Verfahren”. Im oberen Würfel sind ein paar der Grundideen des Gauss-Verfahrens zu erkennen. Die Z-Achse des Würfels definiert eine vorgegebene lineare Abhängigkeit mit Fortschritten in der Erweiterung des linearen Systems. Die X- und Y-Achsen repräsentieren jeweils eine Permutation der Variablen, die in der betreffenden Gleichung aufgelöst wird, und die Diagonalen stellen eindeutige Anordnungen der Variablen des Würfels dar.
Ein elegantes Beispiel ist die einfache Visualisierung namens “Basical Representation of Gauss-Verfahren”. Im oberen Würfel sind ein paar der Grundideen des Gauss-Verfahrens zu erkennen. Die Z-Achse des Würfels definiert eine vorgegebene lineare Abhängigkeit mit Fortschritten in der Erweiterung des linearen Systems. Die X- und Y-Achsen repräsentieren jeweils eine Permutation der Variablen, die in der betreffenden Gleichung aufgelöst wird, und die Diagonalen stellen eindeutige Anordnungen der Variablen des Würfels dar.
Dreiecksformel nach Gauss
Aus den mathematischen Erfindungen von Gauss entwickelte sich ein einfacheres, aber ebenso leistungsfähiges Werkzeug, die sogenannte Dreiecksformel nach Gauss. Diese spezielle Funktion zielt darauf ab, eine Permutation eines Dreiecks zu bestimmen, indem die Seitenlängen des Dreiecks bekannt sind. Die Dreiecksformel nach Gauss bietet die Möglichkeit, die Art und Weise zu bestimmen, in der komplexe Triangelfragmente dargestellt werden können, und die Identifizierung, ob ein Dreieck rechtwinklig oder nicht rechtwinklig ist.
 <small>www.cadmaro.de</small>gauss nach erstellung seite2
Gauss-Verfahren
 www.dieter-heidorn.degauss verfahren aufgelöst gleichung enthält
www.dieter-heidorn.degauss verfahren aufgelöst gleichung enthält
Gauss-Verfahren
 www.dieter-heidorn.degauss verfahren unendlich besitzt lösungen gleichungssystem
www.dieter-heidorn.degauss verfahren unendlich besitzt lösungen gleichungssystem
Visualisierung Des Gauss-Algorithmus
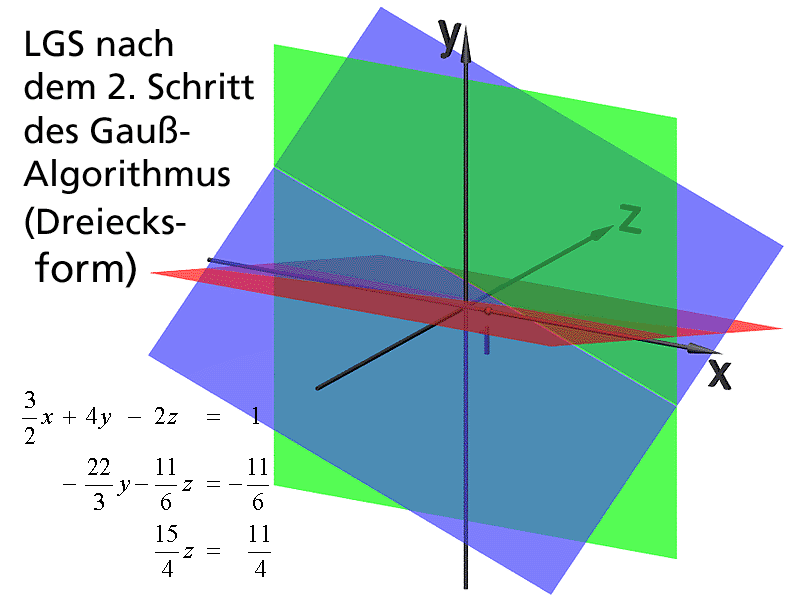 www.mathematik.hu-berlin.degauss schritt nächster vorheriger
www.mathematik.hu-berlin.degauss schritt nächster vorheriger
Dreiecksformel Nach Gauss
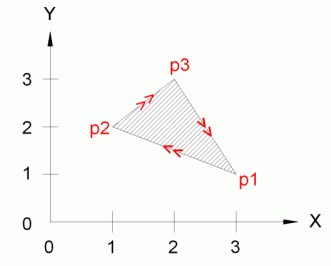 www.cadmaro.degauss 2049
www.cadmaro.degauss 2049
Visualisierung Des Gauss-Algorithmus
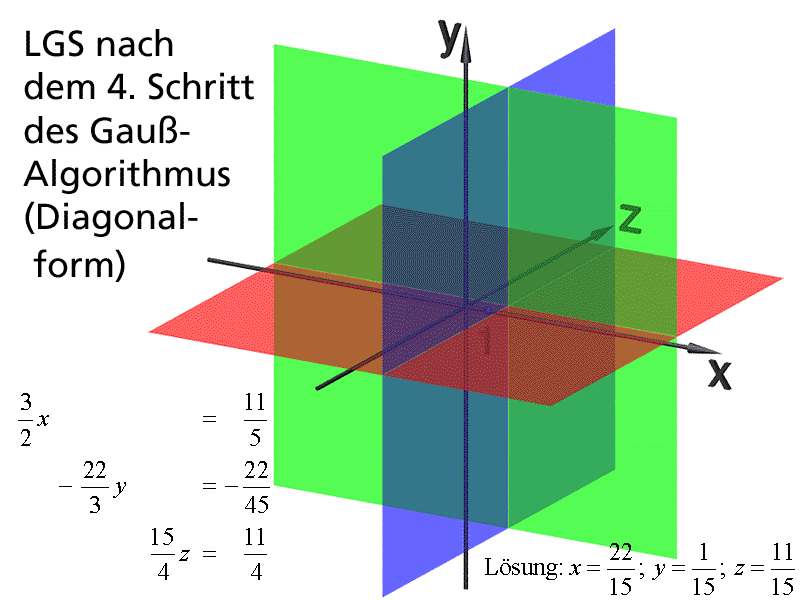 www.mathematik.hu-berlin.degauss algorithmus schritt vorheriger startseite
www.mathematik.hu-berlin.degauss algorithmus schritt vorheriger startseite
Das Gauss-Verfahren
 www.fg.vs.schule-bw.degauss verfahren beispiel
www.fg.vs.schule-bw.degauss verfahren beispiel
U 05.2 – Faltung Einer Gauss-Funktion Mit Sich Selbst | Mathematical
 me-lrt.defaltung funktion gauss lrt
me-lrt.defaltung funktion gauss lrt
Gauß-Algorithmus • Mathe-Brinkmann
 www.brinkmann-du.deVisualisierung des gauss-algorithmus. Dreiecksformel nach gauss. Visualisierung des gauss-algorithmus
www.brinkmann-du.deVisualisierung des gauss-algorithmus. Dreiecksformel nach gauss. Visualisierung des gauss-algorithmus